What do you mean by Tree in data structure in Algorithm?

Question

1. Tree

• What is tree? 
• Figure
• Various terminilogies used

2. Binary Tree

• Its definition
• Basic characteristics of a binary tree
• Basic structure 
• Its properties
• Types of binary tree
• Its representation
• Advantages
• Disadvantages

Answer 1

Tree

What is meant by tree in data structure?

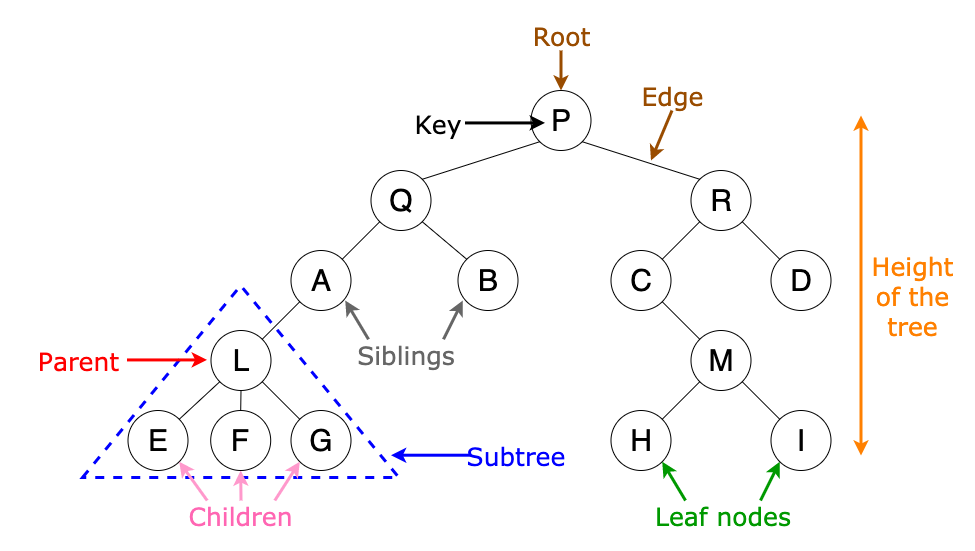
• A tree is a non-linear data structure represented in a hierarchical manner. 
• It contains a finite set of elements called ‘nodes’  
• These are connected to each other using a finite set of directed lines called ‘branches’.
• Children of same parent are called Sibling. 
• Top most element of node is called the root node.  
• The node which do not have any child is called leaf node.
• The node that has atleast one children is called internal node.
• Trees can also called as recursive data structure.

Various Tree terminologies 

Parent:The parent of a node is the immediate predecessor of that node.

Child:The immediate successor of a node are called child nodes. A child nodes which is placed at left side is called left child. A child which is placed at right side is called right side of a node.

Siblings:The child nodes having the same parent is called siblings.

Root:A root is a special designated node in a tree structure. It is a node which has no parent . There can be only one root node in any tree structure.

Leaf nodes(External nodes) :A leaf node which does not have any child nodes.

Internal nodes:Internal nodes which is having a parent and atleast one children are called internal nodes.

Branch and Edge:It is connecting line between two nodes . A node can have more than one edge.

Path:Each node has to be reachable from root to a unique sequence of edges is called a path. The number of edges in a path is called length of the path.

Degree of a node:The number of edges connecting of a particular node is called the degree of a node.

Degree of a tree:The maximum number of a degree of a node is called the degree of a tree.

Level of a node:The level of a node is the number of edges along the unique path between it and the root level of the root is defined as ‘zero’.If a node is at level I, then it childrens is at level I+1.This rule is common for all the nodes except the root node.

Height and depth of a tree: The maximum number of a level of a tree is called its height and depth of a tree. In other words, we can say the height of a Tree is the height of the root node or the depth of the deepest node.

Height of a Node: The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).

Depth of a Node: The depth of a node is the number of edges from the root to the node.

                    

Binary tree

• In binary tree, each node can have atmost two childrens.
• A binary tree, it is either empty or it consists of a node called ‘root node’, it having two childrens, called left subtree and the right subtree of the root

                             Or

A binary tree , it is either empty or it consists of almost two childrens of a node.

Basic structures of Binary Tree

• In this tree, codes either have 0 or 2 children.
• We could have a node with just one child as left child or right child.
• A node with zero childs is called leaf node.

Properties of a Binary Tree:

• A binary tree has n number of nodes, then the number of edges are n-1.
• For a non-empty binary tree ‘n’ is the number of nodes and ‘e’ is number of edges.

             n=e+1

The total number of nodes in a binary tree is atleast 2n +1 and atmost 2n+1+1.

• The minimum number of nodes in a binary tree of height h is ‘h’.
• The number of internal nodes is atleast h and atmost 2h-1.
• The height of a binary tree with n nodes atleast (logn+1) and atmost n.

Types of a Binary tree

We have so many binary trees such as:

• Complete binary tree
• Almost complete binary tree
• Strictly binary tree
• Left skewed binary tree
• Right skewed binary tree

Complete Binary tree

It is a binary tree in which all leaves are at same depth . The total number of nodes at each level has 2i.

• The total number of nodes in a complete binary tree has 2h+1-1,

where h is the height of the tree.

Almost complete binary tree

• It is a binary tree which has two rules:
• Each node has left child, wherever it has a right child that means it is always left child but for a left child there may not be a right child.
• The leaf in a tree must be present at height of h or h-1.

Strictly Binary tree

A binary tree is a strictly binary tree if and only if each node has exactly two child nodes or no nodes.

Left skewed binary tree 

A binary tree is a left skewed binary tree if and only if which is each node having its left child only.

Right skewed Binary tree

A binary tree is a right skewed binary tree if and only if which has each node having its right child only.

Binary tree can be represented in any way of the following two ways:

• Using an array(Linear representation)
• Using a linked list(Linked representation)

• Using an array(Linear representation)

A binary tree can be stored represented by using arrays, which is called sequential or linear represntation. This type of represent is static means that a block of memory for an array is to be accurated before going to store the actual data.

• In this representation, the nodes of the tree are stored level by level starting from the root node . The root node of the tree is stored in the first memory location of allocated memory.
• The following rules are used to decide the location of any node in the tree structure:
• The root node is at location 1.

For any node with index i, 1≤i≤n

a) Parent of (i) =i/2

b) Left child (i) =2i

c) Right child(i) =2i+1

Advantages

• The data are stored without any pointers.
• Any node can be accessed by calculating the indexes.
• Simplicity
• Static memory allocation.

Disadvantages

Array representation is not suitable for normal binary tree, but it is only ideal for complete binary tree.

• Here most of the array a trees are empty means that more memory is wasted unnecessarily.
• Additions and delicious of nodes are inefficient because of the data moments in the array.
• To overcome all these problems by using linked list representation.

Using a linked list representation

• The binary tree can be represented by using dynamic memory allocation of a node in the linked list form. It contains three fields.

a) Info(data) :It contains the actual data of a node.

b) Left link(left) :It contains the address of the left sub- tree.

c) Right link(right) :It contains the address of the right sub-tree.

When a node has no childrens, the corresponding pointers fields(left, right) are “NULL”.

Advantages

• No wastage of memory.
• Insertions and deletions involves no data moment.
• Dynamic memory allocations.

Disadvantages:

• In this the pointer fields occupy more space than data field.
• Programming languages which do not support dynamic memory allocation have difficulty in implementing binary tree.

Answer 2

Python Program to implement General TREE

# Python program to implement Normal Tree 

# TreeNode class that has data and a list of children and parent

class TreeNode:

    def __init__(self, data):

        self.data = data

        self.children = []

        self.parent = None

    #get tree height here

    def get_level(self):

        level = 0

        p = self.parent

        while p:

            level += 1

            p = p.parent

        return level

    #here we will print tree

    def tree_print(self):

        spaces = ' ' * self.get_level() * 3

        prefix = spaces + "|__" if self.parent else ""

        print(prefix + self.data)

        if self.children:

            for child in self.children:

                child.tree_print()

    def add_child(self, child):

        child.parent = self

        self.children.append(child)

def build_ds_tree():

    # create root by making object of Treenode class

    root = TreeNode("Data Structures")

    Primitive = TreeNode("Primitive")

    Primitive.add_child(TreeNode("Integer"))

    Primitive.add_child(TreeNode("Float"))

    Primitive.add_child(TreeNode("Character"))

    NonPrimitive = TreeNode("Non-Primitive")

    

    Linear = TreeNode("Linear")

    Nonlinear = TreeNode("Non-Linear")

    NonPrimitive.add_child(Linear)

    NonPrimitive.add_child(Nonlinear)

    Linear.add_child(TreeNode("Array"))

    Linear.add_child(TreeNode("Linkedlist"))

    Linear.add_child(TreeNode("Stack"))

    Linear.add_child(TreeNode("Queue"))

    

    Nonlinear.add_child(TreeNode("Tree"))

    Nonlinear.add_child(TreeNode("Graph"))

    root.add_child(Primitive)

    root.add_child(NonPrimitive)

    root.tree_print()

#entry point for code execution

if __name__ == '__main__':

    build_ds_tree()

Output-

Data Structures 

|__Primitive 

    |__Integer 

    |__Float 

    |__Character 

|__Non-Primitive 

    |__Linear 

        |__Array 

        |__Linkedlist 

        |__Stack 

        |__Queue 

    |__Non-Linear 

       |__Tree 

       |__Graph